Alternating current bridge methods are of outstanding importance for measurement of electrical quantities.Measurement of inductance,capacitance,storage factor,loss factor may be made conveniently and accurately by employing a.c. bridge networks.
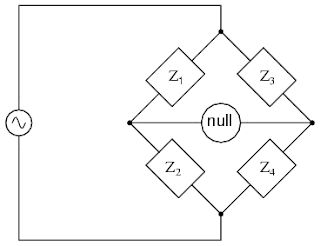
The a.c. bridge is a natural outgrowth of the Wheatstone bridge.An a.c. bridge,in its simplest form, consists of four arms,a source of excitation,and a balance detector.In an a.c. bridge each of the four arms is an impedance,and the battery, and the galvanometer of the Wheatstone bridge are replaced respectively by an a.c. source and detector sensitive to small alternating potential differences.
The useful of a.c. bridge circuits is not restricted to the measurement of unknown impedances and associated parameters like inductance,capacitance,storage factor,dissipation factor etc.These circuits find other applicatithe ons find other applications in communication systems and complex electronic circuits.Alternating current bridge circuits are commonly used for phase shifting,providing feedback paths for oscillators and amplifiers,filtering out undesirable signals and measuring the frequency of audio signals.
General Equation For Bridge Balance
Z1,Z2,Z3,Z4 are the impedances as shown in the circuit diagram above.
The condition for balance that there should be no current through the detector.This requires that the potential difference between points should be zero.This means
potential across Z1 = potential across Z3
on using the above equation and simplifying it we get the following result-:
Z1Z4 = Z2Z3 ,
Thus,using the above equation we can easily solve any kind of a.c. bridges like De Sauty bridge,Anderson's bridge.Above is the general equation.
The a.c. bridge is a natural outgrowth of the Wheatstone bridge.An a.c. bridge,in its simplest form, consists of four arms,a source of excitation,and a balance detector.In an a.c. bridge each of the four arms is an impedance,and the battery, and the galvanometer of the Wheatstone bridge are replaced respectively by an a.c. source and detector sensitive to small alternating potential differences.
The useful of a.c. bridge circuits is not restricted to the measurement of unknown impedances and associated parameters like inductance,capacitance,storage factor,dissipation factor etc.These circuits find other applicatithe ons find other applications in communication systems and complex electronic circuits.Alternating current bridge circuits are commonly used for phase shifting,providing feedback paths for oscillators and amplifiers,filtering out undesirable signals and measuring the frequency of audio signals.
General Equation For Bridge Balance
The condition for balance that there should be no current through the detector.This requires that the potential difference between points should be zero.This means
potential across Z1 = potential across Z3
on using the above equation and simplifying it we get the following result-:
Z1Z4 = Z2Z3 ,
Thus,using the above equation we can easily solve any kind of a.c. bridges like De Sauty bridge,Anderson's bridge.Above is the general equation.
0 comments:
Post a Comment