Monday, September 30, 2013
Wednesday, September 25, 2013
Windows 7 Secrets
download windows 7 secrets
Data Structures Notes
A data structure is a structured set of variables associated with one another in different ways, cooperatively defining components in the system and capable of being operated upon in the program. As stated earlier, the following operations are done on data structures:
- Data organisation or clubbing
- Accessing technique
Net-Guide
This guide is primarily about TCP/IP network protocols and ethernet network architectures, but also
briefly describes other protocol suites, network architectures, and other significant areas of networking.
This guide is written for all audiences, even those with little or no networking experience. It explains in
simple terms the way networks are put together, and how data packages are sent between networks and
subnets along with how data is routed to the internet.
download net-guide
Important Questions of C Programming
C language tricky good pointers questions answers and explanation operators data types arrays structures questions functions recursion preprocessors, looping, file handling, strings questions switch case if else printf advance c linux objective types mcq faq interview questions and answers with explanation and solution for freshers or beginners
download C programming questions
IT Encyclopedia
This IT ENCYCLOPEDIA gives to you a lot of knowledge about the IT fields. there are many topic included like as
programmin
hardware
networking
internet and many more.
download IT ENCYCLOPEDIA
C language topics
here c language is divided in the different different topics like as operators, control statement, input output statement, function, recursion, arrays, structures, pointers etc.
download working with c
Data Structures and alogrithms using c
downloaded data structures using c
"Let Us C" by yashwant kanitkar
download let us c by yashwant kanitkar
Tuesday, September 24, 2013
DISCRTE MATHS
GRAPHS : It is simply a collection of vertices & edges.It can be represented by G(V,E) where V ={v1,v2,.....,vn} & E={e1,e2,......,en}
Here a graph with Vertices v1,v2,v3,v4 & edges e1,e2,e3,e4,e5 is given.
Imp. terms in graphs:
1.Degree :It is defined as no. of edges connected to a particular vertices.It is defined for vertices in graphs.it is represented by d(v).
in above graph d(v1)=d(v4)=3 & d(v2)=d(v3)=2
2.Self loop: when starting & end vertex are same then self loop forms.
For self loop d(v)=2.
3. Parallel edges: If there exists more than one edges b/w any two vertices of graph then those edges are said to be parallel edges.
4.Adjacency: When two vertices are connected through a common edge then those vertices are said to be adjacent &this property is called Adjacency.
TYPES OF GRAPHS
1.Undirected Graph: In a graph G, the set of vertices are V and the set of edges are e and each edge is associated with unordered pair of vertices V, then this graph is known as Undirected Graph. In other words, we can say that each pair of vertices is connected by a straight line and direction between two vertices are not there. for example, the graph G = (Set of vertices, Set of edges) = ({v1, v2, v3}, {e1, e2, e3}). Since, the graph has three vertices so it is a triangular shape as given figure below.
UNDIRECTED GRAPH
2.Directed Graph: A graph is called the Directed Graph if in a graph the set of vertices are V and the set of edges is E, consists the order pairs of elements of V. Generally we can say that each pair of vertices are connected by a straight lines or a direction between both the vertices exist. For example, a graph having the vertices are {v1, v2, v3} and its edges are {e1, e2, e3}). The shape of a graph is a triangular shape. The graph is shown below.
3. Mixed Graph: A mixed graph is the combination of both Directed Graph and Undirected GrapH. A Graph G is knwon as a Mixed Graph if some of the edges in a graph are directed and some are undirected, or we can say that some edges the directions are given and some edges not. For example, a graph with three set of vertices and three edges i.e. G = ({v1, v2, v3}, {e1, e2, e3}) drawn as
Directed Graph
Mixed Graph
4. Null Graph: A graph in which all the verteices are isolated. then it is knwon as a Null graph i.e. a graph has no edges, only vertices called the Null Graph.
Null Graph
5. Simple and Multiple Graph: A graph, in which there is no self loop graph and no parallel edges, then a graph is called a simple graph and a multi graph is a graph with multiple edges between the same vertices.
6. Finite and Infinite Graph: If in a graph G, the set of edges and a vertices are finite then the graph is a finite graph else it is a called as a infinite graph.
Simple and Multiple Graph
Graph 1: Finite Graph Graph 2: Infinite Graph
7. Connected and Disconnected Graph: A vertices are (v1, v2, v3, v4, v5) with the edges (e1, e2, e3, e4, e5, e6, e7, e8).Finite and Infinite Graph
Saturday, September 21, 2013
Maxwell's Inductance Bridge
Maxwell Bridge
and 
can then be calculated based on the values of the other components:
For more assistance kindly refer to given link:-
A Maxwell bridge (in long form, a Maxwell-Wien bridge) is a type of Wheatstone bridge used to measure an unknown inductance(usually of low Q value) in terms of calibrated resistance and capacitance. It is a real product bridge.
It uses the principle that the positive phase angle of an inductive impedance can be compensated by the negative phase angle of a capacitive impedance when put in the opposite arm and the circuit is at resonance; i.e., no potential difference across the detector and hence no current flowing through it. The unknown inductance then becomes known in terms of this capacitance.
With reference to the picture, in a typical application 
and 
are known fixed entities, and 
and 
are known variable entities. and are adjusted until the bridge is balanced.
and are known fixed entities, and and are known variable entities. and are adjusted until the bridge is balanced. and can then be calculated based on the values of the other components:
To avoid the difficulties associated with determining the precise value of a variable capacitance, sometimes a fixed-value capacitor will be installed and more than one resistor will be made variable. It cannot be used for the measurement of high Q values. It is also unsuited for the coils with low Q values, less than one, because of balance convergence problem. Its use is limited to the measurement of low Q values from 1 to 10.
The additional complexity of using a Maxwell bridge over simpler bridge types is warranted in circumstances where either the mutual inductance between the load and the known bridge entities, or stray electromagnetic interference, distorts the measurement results. The capacitive reactance in the bridge will exactly oppose the inductive reactance of the load when the bridge is balanced, allowing the load's resistance and reactance to be reliably determined.
Derivation Of Equation Of Maxwell Bridge
The bridge circuit is used for medium inductance and can be arranged to yield results of considerable precision. As shown in figure 1, in the two arms, there are two pure resistances so that for balance relations, the phase balance depends on the remaining two arms. If a coil of unknown impedance Z1 is placed in one arm, then its positive phase angle ?1 can be compensated for in either of the following two ways:
- A known impedance with an equal positive phase angle may be used in either of the adjacent arms (so that ?1 = ?2 or ?1 = ?4), remaining two arms have zero phase angles (being pure resistances). Such a network is known as Maxwell�s a.c. bridge or L1/L4 bridge.
- Or an impedance with an equal negative phase angle (i.e. capacitance) may be used in opposite arm (so that ?1 + ?3 = 0). Such a network is known as Maxwell-Wien bridge or Maxwell�s L/C bridge.
Hence, we conclude that inductive impedance may be measured in terms of another inductive impedance (of equal time constant) in either adjacent arm (Maxwell Bridge) or the unknown inductive impedance may be measured in terms of a combination of resistance and capacitance (of equal time constant) in the opposite arm (Maxwell-Wien bridge). It is important, however, that in each case the time constants of theThe bridge circuit is used for medium inductance and can be arranged to yield results of considerable precision. As shown in figure 1, in the two arms, there are two pure resistances so that for balance relations, the phase balance depends on the remaining two arms. If a coil of unknown impedance Z1 is placed in one arm, then its positive phase angle ?1 can be compensated for in either of the following two ways:
- A known impedance with an equal positive phase angle may be used in either of the adjacent arms (so that ?1 = ?2 or ?1 = ?4), remaining two arms have zero phase angles (being pure resistances). Such a network is known as Maxwell�s a.c. bridge or L1/L4 bridge.
- Or an impedance with an equal negative phase angle (i.e. capacitance) may be used in opposite arm (so that ?1 + ?3 = 0). Such a network is known as Maxwell-Wien bridge or Maxwell�s L/C bridge.
Hence, we conclude that inductive impedance may be measured in terms of another inductive impedance (of equal time constant) in either adjacent arm (Maxwell Bridge) or the unknown inductive impedance may be measured in terms of a combination of resistance and capacitance (of equal time constant) in the opposite arm (Maxwell-Wien bridge). It is important, however, that in each case the time constants of the two impedance must be matched.As shown in figure 1.
The inductance L4 is a variable self-inductance of constant resistance, its inductance being of the same order as L1. The bridge is balanced by varying L4 and one of the resistance R2 or R3. Alternatively, R2 and R3 can be kept constant and the resistance of one of the other two arms can be varied by connecting an additional resistance in that arm.
The balance condition is that Z1Z3 = Z2Z4
(R1 + j?L1)R3 = (R4 + j?L4)R2
Equation the real and imaginary parts on both sides, we have
R1R3 = R2R4 or R1/R4 = R2/R3
(i.e. products of the resistances of opposite arms are equal).
And
?L1R3 = ?L4R2
Or L1 =L4R2/R3
We can also write that L1 = L�4R1/R4
R1R3 = R2R4 or R1/R4 = R2/R3
(i.e. products of the resistances of opposite arms are equal).
And
?L1R3 = ?L4R2
Or L1 =L4R2/R3
We can also write that L1 = L�4R1/R4
Hence, the unknown self-inductance can be measured in term of the known inductance L4 and the two resistors. Resistive and reactive terms balance independently and the conditions are independent of frequency. This bridge is often used for measuring the iron losses of the transformers at audio frequency.
The balance condition is shown vectorially in figure 2. The current I4 and I3 are in phase with I1 and I2. This is, obviously, brought about by adjusting the impedance of different branches, so these currents lag behind the applied voltage V by the same amount. At balance, the voltage drop V1n across branch 1 is equal to that across branch 4 and I3 = I4. Similarly, voltage drop V2 across branch 2 is equal to that across branch
3 and I1 = I2.
For more assistance kindly refer to given link:-
sensor and instrumentation by Yatika
LVDT (LINEAR VARIABLE DIFFERENTIAL TRANSFORMER).jpg)
This is the most widely used inductive transducer for translating linear motion into an electric signal. The transformer consist of single frequency windings and two secondary widings wound on a cylindrical former. The secondary windings have equal number of turns and are identically placed on either sides of primary windings.The primary windins are connected to an ac source. A movable soft iron core is placed inside the former.The displacement to be measured is applied to the arm attached to the soft iron core. The core is made up of high permeablity nickel iron which is hydrogen annealed.
Since the primary windings is connected by an ac source.It produces an alternating magnetic field which in turn induces an alternating current voltage in the two secondary winding.The output voltage of secondary is ES1 and ES2. In order to converts the outputs into single frequency signal,the two windings are connected in series opposition.The output voltage are
E0=ES1-ES2
When the core is at null position, the flux linking with both the secondary windings are equal.Hence equal emf induced in them.
ES1=ES2
Now if the core moves towards the left of null position,the more flux link with S1 and less with S2
ES2>ES1, E0=ES2-ES1
Ideally, output voltage should be 0 at null position but practically there is a small voltage at output when ES1=ES2 i.e. due to the presence of harmonics in the input supply voltage and also due to the harmonics present in output voltage supply on account of iron core. There may be electric or magnetic unbalance.This voltage is known as Residual voltage
Friday, September 20, 2013
The Hall Effect
The Hall effect is due to the nature of the current in a conductor. Current consists of the movement of many small charge carriers, typically electrons, holes, ions or all three. When a magnetic field is present that is not parallel to the direction of motion of moving charges, these charges experience a force, called the Lorentz force. When such a magnetic field is absent, the charges follow approximately straight, 'line of sight' paths between collisions with impurities, phonons, etc. However, when a magnetic field with a perpendicular component is applied, their paths between collisions are curved so moving charges accumulate on one face of the material. This leaves equal and opposite charges exposed on the other face, where there is a scarcity of mobile charges. The result is an asymmetric distribution of charge density across the Hall element that is perpendicular to both the 'line of sight' path and the applied magnetic field. The separation of charge establishes an electric field that opposes the migration of further charge, so a steady electrical potential is established for as long as the charge is flowing.
When a specimen (metal or semiconductor) carrying a current I is placed in a transverse magnetic field B,then an electric field is induced in the direction perpendicular to both I and B. This phenomena is called Hall Effect.
fig.shows a semiconductor bar carrying a current I in the positive X direction. Let a magnetic field B is applied in the positive Z direction. Now a force is exerted on the charge carries (whether electrons or holes) in the negative Y direction.
Due to this force,moving charges accumulate on one face of the material. This leaves equal and opposite charges exposed on the other face, where there is a scarcity of mobile charges. The result is an asymmetric distribution of charge density across the Hall element that is perpendicular to both the 'line of sight' path and the applied magnetic field. The separation of charge establishes an electric field that opposes the migration of further charge, so a steady electrical potential is established for as long as the charge is flowing.
In equilibrium state,the electric field intensity E due to Hall effect must exerts a force on the carrier which just balances the magnetic force, i.e.,
eE=Bev, (1)
where e is the magnitude of charge on electron or hole and v is the drift velocity.
Now,
E=VH/w
or vH=E*w
since E=B*v
hence VH=Bvw (2)
where w is the distance between two surfaces
We know the current density J is given by
J=I/A=I/tw=nev
v=I/netw (3)
where t is the thickness of the plate and w is the distance between two surfaces
from (2) and (3),we have.
where I is the current across the plate length, B is the magnetic field, t is the thickness of the plate, e is the elementary charge, and n is the charge carrier density of the carrier electrons.
The Hall coefficient is defined as
- where j is the current density of the carrier electrons, and
is the induced electric field. In SI units, this becomes
(The units of RH are usually expressed as m3/C, or O�cm/G, or other variants.) As a result, the Hall effect is very useful as a means to measure either the carrier density or the magnetic field.
One very important feature of the Hall effect is that it differentiates between positive charges moving in one direction and negative charges moving in the opposite. The Hall effect offered the first real proof that electric currents in metals are carried by moving electrons, not by protons. The Hall effect also showed that in some substances (especially p-type semiconductors), it is more appropriate to think of the current as positive "holes" moving rather than negative electrons. A common source of confusion with the Hall Effect is that holes moving to the left are really electrons moving to the right, so one expects the same sign of the Hall coefficient for both electrons and holes. This confusion, however, can only be resolved by modern quantum mechanical theory of transport in solids.
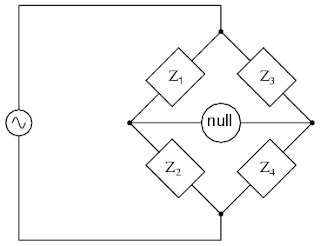
General Equation For A.C. Bridges
Alternating current bridge methods are of outstanding importance for measurement of electrical quantities.Measurement of inductance,capacitance,storage factor,loss factor may be made conveniently and accurately by employing a.c. bridge networks.
The a.c. bridge is a natural outgrowth of the Wheatstone bridge.An a.c. bridge,in its simplest form, consists of four arms,a source of excitation,and a balance detector.In an a.c. bridge each of the four arms is an impedance,and the battery, and the galvanometer of the Wheatstone bridge are replaced respectively by an a.c. source and detector sensitive to small alternating potential differences.
The useful of a.c. bridge circuits is not restricted to the measurement of unknown impedances and associated parameters like inductance,capacitance,storage factor,dissipation factor etc.These circuits find other applicatithe ons find other applications in communication systems and complex electronic circuits.Alternating current bridge circuits are commonly used for phase shifting,providing feedback paths for oscillators and amplifiers,filtering out undesirable signals and measuring the frequency of audio signals.
General Equation For Bridge Balance
Z1,Z2,Z3,Z4 are the impedances as shown in the circuit diagram above.
The condition for balance that there should be no current through the detector.This requires that the potential difference between points should be zero.This means
potential across Z1 = potential across Z3
on using the above equation and simplifying it we get the following result-:
Z1Z4 = Z2Z3 ,
Thus,using the above equation we can easily solve any kind of a.c. bridges like De Sauty bridge,Anderson's bridge.Above is the general equation.
The a.c. bridge is a natural outgrowth of the Wheatstone bridge.An a.c. bridge,in its simplest form, consists of four arms,a source of excitation,and a balance detector.In an a.c. bridge each of the four arms is an impedance,and the battery, and the galvanometer of the Wheatstone bridge are replaced respectively by an a.c. source and detector sensitive to small alternating potential differences.
The useful of a.c. bridge circuits is not restricted to the measurement of unknown impedances and associated parameters like inductance,capacitance,storage factor,dissipation factor etc.These circuits find other applicatithe ons find other applications in communication systems and complex electronic circuits.Alternating current bridge circuits are commonly used for phase shifting,providing feedback paths for oscillators and amplifiers,filtering out undesirable signals and measuring the frequency of audio signals.
General Equation For Bridge Balance
The condition for balance that there should be no current through the detector.This requires that the potential difference between points should be zero.This means
potential across Z1 = potential across Z3
on using the above equation and simplifying it we get the following result-:
Z1Z4 = Z2Z3 ,
Thus,using the above equation we can easily solve any kind of a.c. bridges like De Sauty bridge,Anderson's bridge.Above is the general equation.
STACKS IN DS
Stacks:
A stack is a basic data structure, where insertion and deletion of items takes place at one end called top of the stack. The basic concept can be illustrated by thinking of your data as a stack of plates or books where you can only take the top item off the stack in order to remove things from it.
A stack is also called a LIFO (Last In First Out) to demonstrate the way it accesses data. There are basically three operations that can be performed on stacks . They are 1) inserting an item into a stack (push). 2) deleting an item from the stack (pop). 3) displaying the contents of the stack(pip).
A stack is also called a LIFO (Last In First Out) to demonstrate the way it accesses data. There are basically three operations that can be performed on stacks . They are 1) inserting an item into a stack (push). 2) deleting an item from the stack (pop). 3) displaying the contents of the stack(pip).Algo for push and pop:
Push:
PUSH(STACK,TOP,MAXSTK,ITEM)1: If TOP=MAXSTK,then print OVERFLOW and return.
2:Set TOP=TOP+13:Set STACK
[TOP]=ITEM.
4:Return
Pop:
POP(STACK,TOP,ITEM)1:If TOP=0 then print UNDERFLOW and return.2:Set ITEM=STACK[TOP].3:Set TOP=TOP-1.4:Retun
NOTATIONS IN STACK:
Firstly, we deal with expressions in infix notation
2 + 5
2 5 +
Writing the operators before the operands gives a prefix expression
+2 5
Transforming Infix expressions into Postfix expression:
1. Print operands as they arrive.
2. If the stack is empty or contains a left parenthesis on top, push the incoming operator onto the stack.
3. If the incoming symbol is a left parenthesis, push it on the stack.
4. If the incoming symbol is a right parenthesis, pop the stack and print the operators until you see a left parenthesis. Discard the pair of parentheses.
5. If the incoming symbol has higher precedence than the top of the stack, push it on the stack.
6. If the incoming symbol has equal precedence with the top of the stack, use association. If the association is left to right, pop and print the top of the stack and then push the incoming operator. If the association is right to left, push the incoming operator.
7. If the incoming symbol has lower precedence than the symbol on the top of the stack, pop the stack and print the top operator. Then test the incoming operator against the new top of stack.
8. At the end of the expression, pop and print all operators on the stack. (No parentheses should remain.)
EXAMPLE:
A * (B + C) becomes A B C + *
A subexpression in parentheses must be done before the rest of the expression.
| current symbol | operator stack | postfix string | |
1 | A | A | |
2 | * | * | A |
3 | ( | * ( | A B |
4 | B | * ( | A B |
5 | + | * ( + | A B |
6 | C | * ( + | A B C |
7 | ) | * | A B C + |
8 | A B C + * |
DLD BY SUPRIYA
Consider b1, b2, b3, b4 and b5 is the Binary Number and it is need be converted into Grey Code.
1. In Binary Number Most Significant Bit (MSB) is same as the MSB.
2. By Performing the Exclusive-OR (EX-OR) operation between the First and second bits of the Binary Number the second bit of the Grey code can be found.
3. The Third bit of the Grey code can be found by performing the Exclusive-OR (EX-OR) operation between the Third and Second bits of the given Binary Number; and so on......
To see the video of this topic , please refer to the following link:
To see the video of this topic , please refer to the following link:
EX-OR Operation:
1. The output of EX-OR gate will be 0 if both the bits are 0 or 1 .
2. The output of EX-OR gate will be 1 if one of the bit in two bits which are being added are1 .
Refer the below image for Binary to Gray Code Conversion
Gray Code to Binary Conversion
Consider g0, g1, g2 and g3 is the Grey Code and it is need be converted into Binary Number. The steps for Binary to Grey Code Conversion needs to be reversed to find out the equivalent Binary Number
1.The First MSB of the Grey Codeis same asMost Significant Bit (MSB) of the Binary.
2. If the second Grey Bit is 0 then the second bit of the Binary bit will be same as that of the First Binary bit; AND if the Second Grey Bit is 1 then the Second Bit of the Binary will be inverse of its previous binary bit.
Refer the below image for easy understanding of Grey to Binary Conversion
For more assistance kindly refer to the given link:
Grey Code | Binary to Grey Code and that to Binary Conversion
Excess 3 code Addition & Subtraction
Code is a symbolic representation of discrete information. Codes are of different types. One of the most important codes is Grey Code. It is a non-weighted code which belongs to a class of codes called minimum change codes. While traversing from one step to another step only one bit in the code group changes. In case of Grey Code two adjacent code numbers differs from each other by only one bit.
This code it is not applicable in any types of arithmetical operations but it has some applications in analog to digital converters and in some input/output devices.
There are several steps which will make you understand how the codes are formed:
(1) In case of grey code in each step one bit will change from its previous. One thing must be kept in mind that the change of bit always occurs from the right side i.e from L.S.B towards the M.S.B. At first the first three bits are constant i.e 000 and the fourth bit changes from 0 to 1. As we know that for binary digit possible combination is 0 and 1, so keeping first three bit constant the possible combination of 4th bit is over for decimal 0 and 1 respectively.
(2)Now on moving to the next bit from L.S.B i.e 3rd bit, that changes from 0 to 1 which is the decimal equivalent for 2. And one more combination is left for the fourth bit keeping the first three constant i.e 001. We can change 4th bit from 1 to 0. Thus the grey code for decimal number 3 is 0010.
(3)Traverse to the next code. Here only one thing can be donei.e we can change the second bit as all possible combinations are over.
Question may strike in your mind that why can�t we change the third bit again which will also be a one bit change from its previous.
But changing third bit would give the equivalent grey code 0000 which has occurred earlier. So you must remember that a number occurring previously must not be repeated. So the equivalent code for 4 will be 0110. Here only the second bit has changed from the previous code. Now on keeping first and second bit constant and find the possible combinations of the third and the fourth bit by only changing 1 bit in each steps.
Now for 5 only the fourth bit has changed. Again for 6 only the third bit is changed keeping others constant. Lastly at 7 again the fourth bit has changed from 1 to 0 where all other bits are constant. In 8 you can see that the equivalent grey code is 1100. Here the 1st bit changes from 0 to n1 as all the combination of the 2nd,3rd and 4th bits are completed keeping the 1st constant at 0. Similarly ,the 1st bit is kept constant and all the possible combination changing single bit in each step from right to left is done.
Binary to grey code conversion
Binary to grey code conversion is a very simple process. Several steps are being performed forthis types of conversions. Steps given below elaborate on the idea on this type of conversion.
(1) The first bit of the given binary number will be exactly equal to the M.S.B of the grey code.
(2) Now the second bit of the code will be exclusive-or of the first and second bit of the given binary number, i.e if both the bits are same the result will be 0 and if they are different the result will be 1.
(3)The third bit of grey code will be equal to the exclusive-or of the second and third bit of the given binary number. Thus the conversion goes on. An example given below can make it more clear :
Let (01001) be the given binary number
Thus the equivalent grey code is 01101.
Now lets consider an example where the M.S.B. of the binary is 0 so for it will be 0 for the most significant grey bit. Next, the XOR of the first and the second bit is done. The bits are different so the resultant grey bit will be 1. Now move to the next step, where XOR of second and third bit is again 1 as they are different. Next, XOR of third and fourth bit is 0 as both the bits are same. Lastly the XOR of fourth and fifth bit is 1 as they are different. That is how the result of binary to gray code conversion of 01001 is done whose equivalent grey code is 01101.
Grey code to binary conversion
Grey code to binary conversion is a very simple and easy process. Following thesesteps given below can make it more clear to you:
(1) M.S.B of the given grey code is equal to the M.S.B of the binary number.
(2) Now if the second grey bit is 0 the second binary bit will be same as the previous or the first bit. If the gray bit is 1 the second binary bit will alter. If it was 1 it will be 0 and if it was 0 it will be 1.
(3) This step is repeated for all the bits to do Grey code to binary conversion.
An example given below will make it clear......
Let the grey code be 01101
The M.S.B of the binary will be 0 as the M.S.B of grey is 0. Now moving to the next grey bit. As it is 1 the previous binary bit will alter i.e it will be 1, thus the second binary bit will be 1. Nowlook at the third bit of the grey code. It is again 1 thus the previous bit i.e the second binary bit will again alter and the third bit of the binary number will be 0. Now, 4th bit of the given grey is 0 so the previous binary bit will be unchanged, i.e 4th binary bit will be 0. Now again the 5th grey bit is 1 thus the previous binary bit will alter, it will be 1 from 0. Therefore the equivalent Binary number in case of grey code to binary conversion will be (01001)
Subscribe to:
Posts (Atom)
